A história de topologia
História
A história de topologia
Geometria e Topologia
ETinCiência
Ideias topológicas estão presentes em quase todas as áreas da matemática de hoje. O assunto da topologia em si consiste de vários ramos diferentes, tais como ponto definido, topologia, topologia algébrica e topologia diferencial, que têm relativamente pouco em comum. Devem localizar a ascensão dos conceitos topológicos em um número de diferentes situações.
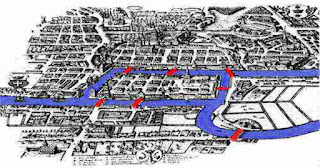
Talvez o primeiro trabalho que merece ser considerada como o início da topologia é devido a Euler. Em 1736, Euler publicou um livro sobre a solução do problema de ponte de Königsberg intitulado Solutio problematis ad geometriam situs pertinentis , que se traduz em inglês como a solução de um problema relacionado com a geometria de posição. O próprio título indica que Euler estava ciente de que ele estava lidando com um tipo diferente de geometria em que a distância não era relevante.
Talvez o primeiro trabalho que merece ser considerada como o início da topologia é devido a Euler. Em 1736, Euler publicou um livro sobre a solução do problema de ponte de Königsberg intitulado Solutio problematis ad geometriam situs pertinentis , que se traduz em inglês como a solução de um problema relacionado com a geometria de posição. O próprio título indica que Euler estava ciente de que ele estava lidando com um tipo diferente de geometria em que a distância não era relevante.
O papel não só mostra que o problema de cruzar as sete pontes em uma única viagem é impossível, mas generaliza o problema para mostrar que, na notação de hoje.
O gráfico tem um caminho a percorrer cada aresta exatamente uma vez tiver exatamente dois vértices de grau ímpar.
O próximo passo para libertar a matemática de ser um assunto sobre medição foi também devido a Euler. Em 1750, ele escreveu uma carta para Christian Goldbach que, assim como comentar sobre uma disputa Goldbach foi ter com um livreiro, dá a famosa fórmula de Eulerpara um poliedro
v - e + f = 2
onde v é o número de vértices do poliedro, e é que o número de arestas e f é o número de faces. É interessante perceber que este, realmente muito simples, a fórmula parece ter sido perdido por Arquimedes e Descartes , embora ambos escreveu extensivamente sobre poliedros. Novamente, a razão deve ser que a todos antes de Euler, tinha sido impossível pensar de Propriedades geométricas sem medição estar envolvida.
Euler publicou detalhes de sua fórmula em 1752 em dois jornais, o primeiro admite que Euler não pode provar o resultado, mas a segunda dá uma prova com base em sólidos dissecação em fatias tetraédricas. Euler tem vista para alguns problemas com sua prova incrivelmente inteligente. Em particular, ele assumiu que os sólidos eram convexos, isto é uma recta que une dois pontos quaisquer sempre está inteiramente dentro do sólido.
O percurso iniciado por Euler com sua fórmula polyhedral seguiu-se um pouco conhecido matemático Lhuilier de Antoine-Jean (1750-1840), que trabalhou durante a maior parte de sua vida em problemas relacionados com a fórmula de Euler.
Em 1813, Lhuilier publicou um trabalho importante. Ele notou que a fórmula de Eulerera errada para sólidos com buracos neles. Se um sólido tem furos g o Lhuilier mostrou que
v - e + f = 2-2g.
Este foi o primeiro resultado conhecido em um invariante topológico.
Möbius publicou uma descrição de uma banda de Möbius em 1865. Ele tentou descrever a propriedade 'unilateral' da banda de Möbius em termos de não-Orientabilidade. Ele pensou a superfície sendo coberta por triângulos orientados. Ele achou que a banda de Möbius não poderia ser enchida com triângulos compatìvel orientados.
Johann Benedict Listing (1802 - 1882) foi o primeiro a usar a topologia de palavra. Listagemde ideias topológicas foram devidas principalmente ao Gauss, embora Gauss ele mesmo optou por não publicar qualquer trabalho na topologia. Listagem escreveu um artigo em 1847 chamado Vorstudien zur Topologie , embora ele já tinha usado a palavra por dez anos na correspondência.
O papel de 1847 não é muito importante, embora ele também introduz a ideia de um complexo, uma vez que é extremamente elementar. Em 1861 listando publicou um papel muito mais importante, no qual ele descreveu a banda de Möbius (4 anos antes de Möbius) e estudou componentes de conectividade e superfícies.
Listagem não foi o primeiro a examinar a conectividade das superfícies. Riemann tinha estudado o conceito em 1851 e, novamente, em 1857, quando ele apresentou as superfícies de Riemann . O problema surgiu de estudar uma equação polinomial f (w, z) = 0 e considerando como as raízes variam como w e z são variáveis. Riemann introduziu superfícies de Riemann , determinadas pela função f (w, z), para que a função w(z) definido pela equação f (w, z) = 0 é o único valor nas superfícies.
Jordan introduziu um outro método para examinar a conectividade de uma superfície. Ele chamou uma simples curva de fechado numa superfície que não se cruzam em si um circuito irredutível se ela não pode ser continuamente transformada em um ponto. Se um circuito geral c pode ser transformado em um sistema de circuitos irredutível um1, ,..., umn para que c descreve umeu m, tempos depois ele escreveu
c = m1um1 + m2a2 +... + mnumn .
O circuito c é redutível se
m 1 um 1 + m2a2 +... + mnumn = 0. (*)
Um sistema de circuitos irredutível um1, ,..., umn é chamado independente se eles satisfazer nenhuma relação do formulário (*) e completa -se qualquer circuito pode ser expressa-los. Jordan provou que o número de circuitos em um conjunto completo e independente é um invariante topológico da superfície.
Listagem tinha examinado conectividade no espaço euclidiano tridimensional, mas Betti estendeu suas ideias para n dimensões. Isto não é tão simples quanto pode parecer desde que mesmo em três dimensões, é possível ter uma superfície que não pode ser reduzida a um ponto ainda fechadas curvas sobre a superfície podem ser reduzidas a um ponto. Definição do Bettide conectividade deixou a desejar e críticas foram feitas por Heegaard.
A ideia de conectividade foi eventualmente, colocar em uma base completamente rigorosa por Poincaré em uma série de papéis situs da análise em 1895. Poincaré introduziu o conceito de homologia e deu um mais precisa definição dos números de Betti associados com um espaço que tinha Betti próprio. Fórmula de poliedros convexos de Eulertinha sido generalizada de poliedros não necessariamente convexos por Jonquières em 1890 e agora Poincaré colocá-lo em um ambiente completamente geral de uma p-dimensional variedade V.
Também enquanto lidava com conectividade Poincaré introduzida o grupo fundamental de uma variedade e a noção de homotopia foi introduzidas nos mesmos jornais 1895.
Uma segunda maneira na qual topologia desenvolvida foi através da generalização das ideias de convergência. Este processo começou realmente em 1817 quando Bolzano remover a associação da convergência com uma sequência de números e convergência associado a qualquer subconjunto infinito limitado de números reais.
Cantor em 1872 introduziu o conceito de conjunto derivado primeiro, o conjunto de pontos de limite, de um conjunto. Ele também definiu fechados subconjuntos da linha real como subconjuntos contendo seu primeiro conjunto de derivada. Cantor também introduziu a ideia de um conjunto aberto de outro conceito fundamental na topologia definida.
Weierstrass em 1877 em um curso de conferências inéditas deu uma rigorosa prova da Bolzano-Weierstrass teorema que afirma que
Um subconjunto infinito limitado S de números reais possui pelo menos um ponto de acumulação de p, ou seja, p satisfaz a propriedade que dado qualquer ε > 0 existe uma sequência infinita (p,n), de pontos de S com | p - pn | < Ε.
Daí, foi introduzido o conceito de vizinhança de um ponto.
Hilbert utilizou o conceito de um bairro em 1902 quando ele respondeu na afirmativa de suas próprias perguntas, nomeadamente
É um grupo de transformação contínua diferenciável?
Em 1906 Fréchet chamado um espaço compacto se qualquer subconjunto infinito limitado contém uma ponto de acumulação. No entanto Fréchet foi capaz de estender o conceito de convergência do espaço euclidiano definindo espaços métricos. Ele também mostrou aquele Cantorde ideias de subconjuntos abertos e fechados, naturalmente estendidos para espaços métricos.
Riesz, em um papel para o Congresso Internacional de matemática em Roma (1909), eliminados completamente da métrica e propôs uma nova abordagem axiomática a topologia. A definição foi baseada em uma definição de conjunto dos pontos de limite, sem noção de distância. Alguns anos mais tarde, em 1914 Hausdorff definido bairros por quatro axiomas então novamente não havia nenhuma métricas considerações. Este trabalho de Riesz e Hausdorff realmente permite a definição de espaços topológicos abstratas.
Há uma terceira maneira no qual conceitos topológicos entraram matemática, nomeadamente através de análise funcional. Este foi um tema que surgiu a física matemática e astronomia, provocada porque os métodos de análise clássica eram um pouco inadequados na luta contra certos tipos de problemas. Jacob Bernoulli e Johann Bernoulli inventaram o cálculo de variações, onde o valor de uma integral é considerado como uma função das funções sendo integrado.
Hadamard introduziu a palavra 'funcional', em 1903, quando estudou funcionais lineares F da forma
F (f) = lim ∫ f (x) gn(x) dx
onde o limite é tomado como n → ∞ e a integral é de a para b. Fréchet continuou o desenvolvimento funcional, definindo a derivada de uma funcional em 1904. Schmidt em 1907 examinou a noção de convergência em espaços de sequência, estendendo-se métodos que Hilbert tinha usado em sua obra sobre equações integrais para generalizar a ideia de uma série de Fourier . Distância foi definida através de um produto interno.
Schmidtdo trabalho em espaços de sequência tem análogos na teoria das funções de quadrado somável, este trabalho sendo feito também em 1907 por Schmidt se e independentemente por Fréchet.
Mais um passo na abstração foi tirado por Banach em 1932, quando se mudou de produto interno espaços para espaços normados. Banach levou funcionais lineares de Fréchete mostrou que eles tinham um cenário natural em espaços normados.
Poincaré desenvolveu muitos de seus métodos topológicos estudando equações diferenciais ordinárias, que surgiu a partir de um estudo de certos problemas de astronomia. O estudo de sistemas autônomos
dx/dt = f (x, y), dy/dt = g(x, y)
envolveu-se olhando para a totalidade de todas as soluções em vez de em trajetórias particulares como foi o caso mais cedo. A coleção de métodos desenvolvidos por Poincaré foi construída em uma completa teoria topológica de Brouwer em 1912.
O gráfico tem um caminho a percorrer cada aresta exatamente uma vez tiver exatamente dois vértices de grau ímpar.
O próximo passo para libertar a matemática de ser um assunto sobre medição foi também devido a Euler. Em 1750, ele escreveu uma carta para Christian Goldbach que, assim como comentar sobre uma disputa Goldbach foi ter com um livreiro, dá a famosa fórmula de Eulerpara um poliedro
v - e + f = 2
onde v é o número de vértices do poliedro, e é que o número de arestas e f é o número de faces. É interessante perceber que este, realmente muito simples, a fórmula parece ter sido perdido por Arquimedes e Descartes , embora ambos escreveu extensivamente sobre poliedros. Novamente, a razão deve ser que a todos antes de Euler, tinha sido impossível pensar de Propriedades geométricas sem medição estar envolvida.
Euler publicou detalhes de sua fórmula em 1752 em dois jornais, o primeiro admite que Euler não pode provar o resultado, mas a segunda dá uma prova com base em sólidos dissecação em fatias tetraédricas. Euler tem vista para alguns problemas com sua prova incrivelmente inteligente. Em particular, ele assumiu que os sólidos eram convexos, isto é uma recta que une dois pontos quaisquer sempre está inteiramente dentro do sólido.
O percurso iniciado por Euler com sua fórmula polyhedral seguiu-se um pouco conhecido matemático Lhuilier de Antoine-Jean (1750-1840), que trabalhou durante a maior parte de sua vida em problemas relacionados com a fórmula de Euler.
Em 1813, Lhuilier publicou um trabalho importante. Ele notou que a fórmula de Eulerera errada para sólidos com buracos neles. Se um sólido tem furos g o Lhuilier mostrou que
v - e + f = 2-2g.
Este foi o primeiro resultado conhecido em um invariante topológico.
Möbius publicou uma descrição de uma banda de Möbius em 1865. Ele tentou descrever a propriedade 'unilateral' da banda de Möbius em termos de não-Orientabilidade. Ele pensou a superfície sendo coberta por triângulos orientados. Ele achou que a banda de Möbius não poderia ser enchida com triângulos compatìvel orientados.
Johann Benedict Listing (1802 - 1882) foi o primeiro a usar a topologia de palavra. Listagemde ideias topológicas foram devidas principalmente ao Gauss, embora Gauss ele mesmo optou por não publicar qualquer trabalho na topologia. Listagem escreveu um artigo em 1847 chamado Vorstudien zur Topologie , embora ele já tinha usado a palavra por dez anos na correspondência.
O papel de 1847 não é muito importante, embora ele também introduz a ideia de um complexo, uma vez que é extremamente elementar. Em 1861 listando publicou um papel muito mais importante, no qual ele descreveu a banda de Möbius (4 anos antes de Möbius) e estudou componentes de conectividade e superfícies.
Listagem não foi o primeiro a examinar a conectividade das superfícies. Riemann tinha estudado o conceito em 1851 e, novamente, em 1857, quando ele apresentou as superfícies de Riemann . O problema surgiu de estudar uma equação polinomial f (w, z) = 0 e considerando como as raízes variam como w e z são variáveis. Riemann introduziu superfícies de Riemann , determinadas pela função f (w, z), para que a função w(z) definido pela equação f (w, z) = 0 é o único valor nas superfícies.
Jordan introduziu um outro método para examinar a conectividade de uma superfície. Ele chamou uma simples curva de fechado numa superfície que não se cruzam em si um circuito irredutível se ela não pode ser continuamente transformada em um ponto. Se um circuito geral c pode ser transformado em um sistema de circuitos irredutível um1, ,..., umn para que c descreve umeu m, tempos depois ele escreveu
c = m1um1 + m2a2 +... + mnumn .
O circuito c é redutível se
m 1 um 1 + m2a2 +... + mnumn = 0. (*)
Um sistema de circuitos irredutível um1, ,..., umn é chamado independente se eles satisfazer nenhuma relação do formulário (*) e completa -se qualquer circuito pode ser expressa-los. Jordan provou que o número de circuitos em um conjunto completo e independente é um invariante topológico da superfície.
Listagem tinha examinado conectividade no espaço euclidiano tridimensional, mas Betti estendeu suas ideias para n dimensões. Isto não é tão simples quanto pode parecer desde que mesmo em três dimensões, é possível ter uma superfície que não pode ser reduzida a um ponto ainda fechadas curvas sobre a superfície podem ser reduzidas a um ponto. Definição do Bettide conectividade deixou a desejar e críticas foram feitas por Heegaard.
A ideia de conectividade foi eventualmente, colocar em uma base completamente rigorosa por Poincaré em uma série de papéis situs da análise em 1895. Poincaré introduziu o conceito de homologia e deu um mais precisa definição dos números de Betti associados com um espaço que tinha Betti próprio. Fórmula de poliedros convexos de Eulertinha sido generalizada de poliedros não necessariamente convexos por Jonquières em 1890 e agora Poincaré colocá-lo em um ambiente completamente geral de uma p-dimensional variedade V.
Também enquanto lidava com conectividade Poincaré introduzida o grupo fundamental de uma variedade e a noção de homotopia foi introduzidas nos mesmos jornais 1895.
Uma segunda maneira na qual topologia desenvolvida foi através da generalização das ideias de convergência. Este processo começou realmente em 1817 quando Bolzano remover a associação da convergência com uma sequência de números e convergência associado a qualquer subconjunto infinito limitado de números reais.
Cantor em 1872 introduziu o conceito de conjunto derivado primeiro, o conjunto de pontos de limite, de um conjunto. Ele também definiu fechados subconjuntos da linha real como subconjuntos contendo seu primeiro conjunto de derivada. Cantor também introduziu a ideia de um conjunto aberto de outro conceito fundamental na topologia definida.
Weierstrass em 1877 em um curso de conferências inéditas deu uma rigorosa prova da Bolzano-Weierstrass teorema que afirma que
Um subconjunto infinito limitado S de números reais possui pelo menos um ponto de acumulação de p, ou seja, p satisfaz a propriedade que dado qualquer ε > 0 existe uma sequência infinita (p,n), de pontos de S com | p - pn | < Ε.
Daí, foi introduzido o conceito de vizinhança de um ponto.
Hilbert utilizou o conceito de um bairro em 1902 quando ele respondeu na afirmativa de suas próprias perguntas, nomeadamente
É um grupo de transformação contínua diferenciável?
Em 1906 Fréchet chamado um espaço compacto se qualquer subconjunto infinito limitado contém uma ponto de acumulação. No entanto Fréchet foi capaz de estender o conceito de convergência do espaço euclidiano definindo espaços métricos. Ele também mostrou aquele Cantorde ideias de subconjuntos abertos e fechados, naturalmente estendidos para espaços métricos.
Riesz, em um papel para o Congresso Internacional de matemática em Roma (1909), eliminados completamente da métrica e propôs uma nova abordagem axiomática a topologia. A definição foi baseada em uma definição de conjunto dos pontos de limite, sem noção de distância. Alguns anos mais tarde, em 1914 Hausdorff definido bairros por quatro axiomas então novamente não havia nenhuma métricas considerações. Este trabalho de Riesz e Hausdorff realmente permite a definição de espaços topológicos abstratas.
Há uma terceira maneira no qual conceitos topológicos entraram matemática, nomeadamente através de análise funcional. Este foi um tema que surgiu a física matemática e astronomia, provocada porque os métodos de análise clássica eram um pouco inadequados na luta contra certos tipos de problemas. Jacob Bernoulli e Johann Bernoulli inventaram o cálculo de variações, onde o valor de uma integral é considerado como uma função das funções sendo integrado.
Hadamard introduziu a palavra 'funcional', em 1903, quando estudou funcionais lineares F da forma
F (f) = lim ∫ f (x) gn(x) dx
onde o limite é tomado como n → ∞ e a integral é de a para b. Fréchet continuou o desenvolvimento funcional, definindo a derivada de uma funcional em 1904. Schmidt em 1907 examinou a noção de convergência em espaços de sequência, estendendo-se métodos que Hilbert tinha usado em sua obra sobre equações integrais para generalizar a ideia de uma série de Fourier . Distância foi definida através de um produto interno.
Schmidtdo trabalho em espaços de sequência tem análogos na teoria das funções de quadrado somável, este trabalho sendo feito também em 1907 por Schmidt se e independentemente por Fréchet.
Mais um passo na abstração foi tirado por Banach em 1932, quando se mudou de produto interno espaços para espaços normados. Banach levou funcionais lineares de Fréchete mostrou que eles tinham um cenário natural em espaços normados.
Poincaré desenvolveu muitos de seus métodos topológicos estudando equações diferenciais ordinárias, que surgiu a partir de um estudo de certos problemas de astronomia. O estudo de sistemas autônomos
dx/dt = f (x, y), dy/dt = g(x, y)
envolveu-se olhando para a totalidade de todas as soluções em vez de em trajetórias particulares como foi o caso mais cedo. A coleção de métodos desenvolvidos por Poincaré foi construída em uma completa teoria topológica de Brouwer em 1912.
O ensino da matemática na Roma antiga
CMisteriosBlog
O artigo é uma tradução do conteúdo deste página: History MCS ST Andrews - A history of Topology. O conteúdo pode ser editado para estilo e tamanho.