Geometria não-euclidiana
História
Geometria não-euclidiana
Geometria e Topologia
ETinCiencia
Em cerca de 300 a.C., Euclid's escreveu Os elementos, um livro que se tornaria um dos mais famosos livros já escritos. Euclid's declarou cinco postulados em que ele baseia todos os seus teoremas:
⦁ Desenhar uma linha reta de qualquer ponto a qualquer outro.
⦁ Para produzir uma linha reta finita continuamente numa linha recta.
⦁ Para descrever um círculo com qualquer centro e distância.
⦁ Que todos os ângulos retos são iguais entre si.
⦁ Desenhar uma linha reta de qualquer ponto a qualquer outro.
⦁ Para produzir uma linha reta finita continuamente numa linha recta.
⦁ Para descrever um círculo com qualquer centro e distância.
⦁ Que todos os ângulos retos são iguais entre si.
Que, se uma linha reta caindo em duas linhas retas faz os ângulos internos no mesmo lado inferior a dois ângulos retos, se produzidas indefinidamente, encontrar do outro lado em que são os ângulos menos do que os dois ângulos retos.
É claro que o quinto postulado é diferente dos outros quatro. Não satisfez Euclid's e tentou evitar a sua utilização, tanto quanto possível - na verdade, as primeiro 28 proposições dos Elementos a são provou sem usá-lo. Outro comentário vale a pena fazer neste momento é que Euclid's, e muitos que estavam a segui-lo, supôs-se que linhas retas eram infinitas.
Proclo (410-485) escreveu um comentário sobre Os elementos onde ele comenta sobre tentativa de quatro provas para deduzir o quinto postulado do outro, em particular, ele observa que Ptolemy tinha produzido um falso 'prova'. Proclus então passa a dar uma prova falsa da sua própria. No entanto, ele deu o seguinte postulado que é equivalente para o quinto postulado.
Axioma do Playfair:- dada uma linha e um ponto não em linha, é possível desenhar exatamente uma linha através do ponto determinado paralelo à linha.
Embora conhecido desde o tempo de Proclus, isto se tornou conhecido como Axioma do Playfair depois John Playfair escreveu um comentário famoso sobre Euclid's , em 1795, onde ele propôs a substituição de Euclid'squinto postulado por este axioma.
Muitas tentativas foram feitas para provar o quinto postulado de outros quatro, muitos deles sendo aceitos como provas por longos períodos de tempo até que o erro foi encontrado. Invariavelmente, o erro foi assumindo alguma propriedade 'óbvia' que acabou por ser equivalente ao quinto postulado. Tal 'prova' foi dado por Wallis em 1663, quando pensou que ele tinha deduzido o quinto postulado, mas ele realmente tinha mostrado que seja equivalente a:
Para cada triângulo, existe um triângulo semelhante magnitude arbitrário.
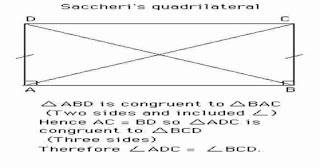
Uma das provas tentativas acabou por ser mais importante do que a maioria dos outros. Foi produzido em 1697 por Girolamo Saccheri. A importância do trabalho de Saccherifoi que ele assumiu o quinto falso postulado e tentou derivar uma contradição.
Aqui é o Quadrilátero Saccheri
Nesta figura Saccheri provou que os ângulos de Cimeira em D e C eram iguais. A prova usa propriedades de triângulos congruentes que Euclid's provou em proposições quatro e oito que são provados antes do quinto postulado é usado. Saccheri tem mostrado:
a) São os ângulos de Cimeira > 90° (hipótese do ângulo obtuso).
b) os ângulos Cimeira são < 90° (hipótese do ângulo agudo).
c) os ângulos de Cimeira são = 90° (hipótese do ângulo reto).
Quinto postulado de Euclid's é c ). Saccheri provou que a hipótese do ângulo obtuso implicava o quinto postulado, obtendo assim uma contradição. Saccheri, em seguida, estudou a hipótese de um ângulo agudo e derivados muitos teoremas de geometria não-euclidiana, sem perceber que ele estava fazendo. No entanto ele eventualmente 'provou' que a hipótese do ângulo agudo levou a uma contradição por supondo que há um “ponto no infinito’ que se encontra em um avião”.
Em 1766 Lambert seguiu uma linha semelhante de Saccheri. No entanto ele não caiu na armadilha que Saccheri caiu e investigou a hipótese de um ângulo agudo sem obter uma contradição. Lambert, notado nesta nova geometria, a soma do ângulo de um triângulo aumentada como a área do triângulo diminuída.
Legendre passou 40 anos de sua vida trabalhando sobre o postulado do paralelo e o trabalho aparece em apêndices para várias edições de seu livro de geometria altamente bem sucedido Eléments de Géométrie. Legendre , provou que o quinto postulado de Euclid'sné equivalente a:
A soma dos ângulos de um triângulo é igual a dois ângulos retos.
Legendre mostrou como Saccheri tinha mais de 100 anos antes, que a soma dos ângulos de um triângulo não pode ser superior a dois ângulos retos. Isso, novamente como Saccheri, repousava sobre o fato de que as linhas retas eram infinitas. Na tentativa de mostrar que o ângulo soma não pode ser inferior a 180° Legendre assumiu através de qualquer ponto no interior de um ângulo é sempre possível traçar uma linha que atende a ambos os lados do ângulo. Isto acaba por ser de outra forma equivalente do quinto postulado, mas Legendre nunca percebeu seu erro próprio.
Geometria elementar foi por esse tempo envolvido em problemas do postulado do paralelo. D'Alembert, em 1767, chamado o escândalo da geometria elementar.
A primeira pessoa que realmente vir a entender o problema dos paralelos foi Gauss. Começou a trabalhar no quinto postulado em 1792, enquanto apenas 15 anos de idade, na primeira tentativa de provar o postulado das paralelas dos outros quatro. Por 1813 ele tinha feito pouco progresso e escreveu:
Na teoria dos paralelos, até agora não estamos mais longe do que Euclid's. Esta é uma parte vergonhosa da matemática...
No entanto por 1817 Gauss tinha-se convencido de que o quinto postulado era independente dos outros quatro postulados. Ele começou a trabalhar para as consequências de uma geometria em que mais de uma linha pode ser desenhada através de um determinado ponto paralelo para uma determinada linha. Talvez mais surpreendentemente de todos Gauss nunca publicou este trabalho, mas manteve em segredo. Neste momento pensar foi dominado por Kant, que havia afirmado que a geometria euclidiana é a inevitável necessidade de pensamento e Gauss não gostava de controvérsia.
Gauss sobre a teoria dos paralelos com seu amigo, o matemático Farkas Bolyai, que fez várias provas falsas do postulado da paralela. Farkas Bolyai ensinou matemática seu filho, János Bolyai, mas, apesar de aconselhando seu filho para não desperdiçar uma hora naquele problema do problema do quinto postulado, János Bolyai trabalhar sobre o problema.
Em 1823, János Bolyai escreveu ao pai dizendo descobri coisas tão maravilhoso que fiquei surpreendido... do nada eu criei um estranho mundo novo. No entanto, demorou Bolyai mais dois anos, antes de tudo o que foi escrito para baixo e ele publicou seu estranho mundo novo como um apêndice de 24 páginas para o livro do seu pai, embora só para confundir as gerações futuras o apêndice foi publicado antes do livro em si.
Gauss, depois de ler as 24 páginas, descrito János Bolyai nestas palavras ao escrever para um amigo: eu considero este geômetra jovem Bolyai como um gênio de primeira ordem. No entanto em algum sentido Bolyai assumiu apenas que a nova geometria era possível. Ele então seguiu as consequências de uma forma não muito diferente daqueles que tinha escolhido para assumir que o quinto postulado era falso e procurar uma contradição. No entanto, o verdadeiro avanço foi a crença de que a nova geometria era possível. Gauss, no entanto impressionado ele soou na citação acima com Bolyai, bastante devastada Bolyai dizendo-lhe que ele (Gauss) tinha descoberto tudo isso antes, mas não tinha publicado. Embora isto, sem dúvida, deve ter sido verdade, ele diminui em nenhuma maneira Bolyai do avanço notável.
Nem é o trabalho do Bolyai diminuído porque Lobachevsky publicou um trabalho sobre geometria não-euclidiana em 1829. Bolyai , nem Gauss sabia de Lobachevskydo trabalho, principalmente porque só foi publicado em Russo no Mensageiro de Kazan uma publicação da Universidade local. Lobachevskya tentativa de atingir um público maior tinha falhado quando seu papel foi rejeitado por Ostrogradski.
Na verdade Lobachevsky saíram nada melhor do que Bolyai em ganhar o reconhecimento público pelo seu importante trabalho. Ele publicou investigações geométricas sobre a teoria dos paralelos em 1840 que, nas suas 61 páginas, dão a conta mais clara de Lobachevskydo trabalho. A publicação de uma conta em francês no jornal de Crelleem 1837 trouxe seu trabalho em geometria não-euclidiana para um público amplo, mas a Comunidade matemática não estava pronta para aceitar ideias tão revolucionárias.
Lobachevskydo livreto de 1840 ele explica claramente como funciona sua geometria não-euclidiana.
Todas as linhas retas que, em um avião, sair de um ponto podem, com referência a uma determinada linha reta no mesmo plano, ser divididas em duas classes - em corte e non-corte. As linhas de delimitação do e a outra classe dessas linhas serão chamadas paralelas à linha determinada.
Aqui está o diagrama do Lobachevsky
Portanto, Lobachevsky substituiu o quinto postulado de Euclid's por:
Postulado das paralelas do Lobachevsky. Existem duas linhas paralelas para uma determinada linha através de um determinado ponto não na linha.
Lobachevsky passou a desenvolver muitas identidades trigonométricas de triângulos que realizou nesta geometria, mostrando que, como o triângulo tornou-se pequeno as identidades tendiam às identidades trigonométricas usuais.
Riemann, que escreveu sua tese de doutorado sob a supervisão de Gauss, deu uma palestra inaugural em 10 de junho de 1854, em que ele reformulou todo o conceito da geometria que ele via como um espaço com bastante estrutura extra para ser capaz de medir coisas como comprimento. Esta palestra não foi publicada até 1868, dois anos após a morte de Riemann mas era ter uma profunda influência sobre o desenvolvimento de uma riqueza de diferentes geometrias. Riemann brevemente discutidos uma geometria 'esférica', em que cada linha através de um ponto P, não em uma linha AB atende a linha AB. Nesta geometria não paralelos são possíveis.
É importante perceber que Bolyaido nem Lobachevskya descrição de sua nova geometria tinha sido provou para ser consistente. Na verdade não foi diferente da geometria euclidiana, a este respeito, apesar dos muitos séculos de trabalho com a geometria euclidiana foi suficiente para convencer os matemáticos que não há contradição alguma vez aparecem dentro dele.
A primeira pessoa a colocar a Bolyai - geometria não-euclidiana Lobachevsky no mesmo patamar que a geometria euclidiana era Eugenio Beltrami (1835-1900). Em 1868 ele escreveu um livro de ensaio sobre a interpretação da geometria não-euclidiana que produziu um modelo para a geometria não-euclidiana 2-dimensional dentro de 3-dimensional geometria euclidiana. O modelo obteve-se sobre a superfície de revolução de um tractrix sobre sua assíntota. Isso às vezes é chamado um pseudo-esfera.
Você pode ver o gráfico de um tractrix e parece que a metade superior de uma esfera de pseudo.
Na verdade Beltramido modelo estava incompleto, mas certamente deu uma decisão definitiva sobre o quinto postulado de Euclid's desde o modelo fornecido uma configuração na qual Euclid's de quatro primeiros postulados realizada, mas o quinto não segurou. Reduziu o problema da consistência dos axiomas da geometria não-euclidiana, a que da consistência dos axiomas da geometria euclidiana.
Beltramido trabalho em um modelo de Bolyai - geometria não-euclidiana do Lobachevskyfoi completado por Klein em 1871. Klein foi mais longe e deu modelos de outras geometrias não euclidianas como Geometria esférica de Riemann. Kleindo trabalho foi baseado em uma noção de distância definida por Cayley em 1859, quando ele propôs uma definição generalizada para a distância.
Klein mostrou que existem três tipos basicamente diferentes da geometria. Na Bolyai - Lobachevsky tipo de geometria, linhas retas tem dois pontos infinitamente distantes. O tipo de Riemann de Geometria esférica, linhas não têm (ou mais precisamente dois imaginários) pontos infinitamente distantes. Geometria euclidiana é um caso limite entre os dois, onde para cada linha existem dois pontos infinitamente distantes coincidentes.
É claro que o quinto postulado é diferente dos outros quatro. Não satisfez Euclid's e tentou evitar a sua utilização, tanto quanto possível - na verdade, as primeiro 28 proposições dos Elementos a são provou sem usá-lo. Outro comentário vale a pena fazer neste momento é que Euclid's, e muitos que estavam a segui-lo, supôs-se que linhas retas eram infinitas.
Proclo (410-485) escreveu um comentário sobre Os elementos onde ele comenta sobre tentativa de quatro provas para deduzir o quinto postulado do outro, em particular, ele observa que Ptolemy tinha produzido um falso 'prova'. Proclus então passa a dar uma prova falsa da sua própria. No entanto, ele deu o seguinte postulado que é equivalente para o quinto postulado.
Axioma do Playfair:- dada uma linha e um ponto não em linha, é possível desenhar exatamente uma linha através do ponto determinado paralelo à linha.
Embora conhecido desde o tempo de Proclus, isto se tornou conhecido como Axioma do Playfair depois John Playfair escreveu um comentário famoso sobre Euclid's , em 1795, onde ele propôs a substituição de Euclid'squinto postulado por este axioma.
Muitas tentativas foram feitas para provar o quinto postulado de outros quatro, muitos deles sendo aceitos como provas por longos períodos de tempo até que o erro foi encontrado. Invariavelmente, o erro foi assumindo alguma propriedade 'óbvia' que acabou por ser equivalente ao quinto postulado. Tal 'prova' foi dado por Wallis em 1663, quando pensou que ele tinha deduzido o quinto postulado, mas ele realmente tinha mostrado que seja equivalente a:
Para cada triângulo, existe um triângulo semelhante magnitude arbitrário.
Uma das provas tentativas acabou por ser mais importante do que a maioria dos outros. Foi produzido em 1697 por Girolamo Saccheri. A importância do trabalho de Saccherifoi que ele assumiu o quinto falso postulado e tentou derivar uma contradição.
Aqui é o Quadrilátero Saccheri
Nesta figura Saccheri provou que os ângulos de Cimeira em D e C eram iguais. A prova usa propriedades de triângulos congruentes que Euclid's provou em proposições quatro e oito que são provados antes do quinto postulado é usado. Saccheri tem mostrado:
a) São os ângulos de Cimeira > 90° (hipótese do ângulo obtuso).
b) os ângulos Cimeira são < 90° (hipótese do ângulo agudo).
c) os ângulos de Cimeira são = 90° (hipótese do ângulo reto).
Quinto postulado de Euclid's é c ). Saccheri provou que a hipótese do ângulo obtuso implicava o quinto postulado, obtendo assim uma contradição. Saccheri, em seguida, estudou a hipótese de um ângulo agudo e derivados muitos teoremas de geometria não-euclidiana, sem perceber que ele estava fazendo. No entanto ele eventualmente 'provou' que a hipótese do ângulo agudo levou a uma contradição por supondo que há um “ponto no infinito’ que se encontra em um avião”.
Em 1766 Lambert seguiu uma linha semelhante de Saccheri. No entanto ele não caiu na armadilha que Saccheri caiu e investigou a hipótese de um ângulo agudo sem obter uma contradição. Lambert, notado nesta nova geometria, a soma do ângulo de um triângulo aumentada como a área do triângulo diminuída.
Legendre passou 40 anos de sua vida trabalhando sobre o postulado do paralelo e o trabalho aparece em apêndices para várias edições de seu livro de geometria altamente bem sucedido Eléments de Géométrie. Legendre , provou que o quinto postulado de Euclid'sné equivalente a:
A soma dos ângulos de um triângulo é igual a dois ângulos retos.
Legendre mostrou como Saccheri tinha mais de 100 anos antes, que a soma dos ângulos de um triângulo não pode ser superior a dois ângulos retos. Isso, novamente como Saccheri, repousava sobre o fato de que as linhas retas eram infinitas. Na tentativa de mostrar que o ângulo soma não pode ser inferior a 180° Legendre assumiu através de qualquer ponto no interior de um ângulo é sempre possível traçar uma linha que atende a ambos os lados do ângulo. Isto acaba por ser de outra forma equivalente do quinto postulado, mas Legendre nunca percebeu seu erro próprio.
Geometria elementar foi por esse tempo envolvido em problemas do postulado do paralelo. D'Alembert, em 1767, chamado o escândalo da geometria elementar.
A primeira pessoa que realmente vir a entender o problema dos paralelos foi Gauss. Começou a trabalhar no quinto postulado em 1792, enquanto apenas 15 anos de idade, na primeira tentativa de provar o postulado das paralelas dos outros quatro. Por 1813 ele tinha feito pouco progresso e escreveu:
Na teoria dos paralelos, até agora não estamos mais longe do que Euclid's. Esta é uma parte vergonhosa da matemática...
No entanto por 1817 Gauss tinha-se convencido de que o quinto postulado era independente dos outros quatro postulados. Ele começou a trabalhar para as consequências de uma geometria em que mais de uma linha pode ser desenhada através de um determinado ponto paralelo para uma determinada linha. Talvez mais surpreendentemente de todos Gauss nunca publicou este trabalho, mas manteve em segredo. Neste momento pensar foi dominado por Kant, que havia afirmado que a geometria euclidiana é a inevitável necessidade de pensamento e Gauss não gostava de controvérsia.
Gauss sobre a teoria dos paralelos com seu amigo, o matemático Farkas Bolyai, que fez várias provas falsas do postulado da paralela. Farkas Bolyai ensinou matemática seu filho, János Bolyai, mas, apesar de aconselhando seu filho para não desperdiçar uma hora naquele problema do problema do quinto postulado, János Bolyai trabalhar sobre o problema.
Em 1823, János Bolyai escreveu ao pai dizendo descobri coisas tão maravilhoso que fiquei surpreendido... do nada eu criei um estranho mundo novo. No entanto, demorou Bolyai mais dois anos, antes de tudo o que foi escrito para baixo e ele publicou seu estranho mundo novo como um apêndice de 24 páginas para o livro do seu pai, embora só para confundir as gerações futuras o apêndice foi publicado antes do livro em si.
Gauss, depois de ler as 24 páginas, descrito János Bolyai nestas palavras ao escrever para um amigo: eu considero este geômetra jovem Bolyai como um gênio de primeira ordem. No entanto em algum sentido Bolyai assumiu apenas que a nova geometria era possível. Ele então seguiu as consequências de uma forma não muito diferente daqueles que tinha escolhido para assumir que o quinto postulado era falso e procurar uma contradição. No entanto, o verdadeiro avanço foi a crença de que a nova geometria era possível. Gauss, no entanto impressionado ele soou na citação acima com Bolyai, bastante devastada Bolyai dizendo-lhe que ele (Gauss) tinha descoberto tudo isso antes, mas não tinha publicado. Embora isto, sem dúvida, deve ter sido verdade, ele diminui em nenhuma maneira Bolyai do avanço notável.
Nem é o trabalho do Bolyai diminuído porque Lobachevsky publicou um trabalho sobre geometria não-euclidiana em 1829. Bolyai , nem Gauss sabia de Lobachevskydo trabalho, principalmente porque só foi publicado em Russo no Mensageiro de Kazan uma publicação da Universidade local. Lobachevskya tentativa de atingir um público maior tinha falhado quando seu papel foi rejeitado por Ostrogradski.
Na verdade Lobachevsky saíram nada melhor do que Bolyai em ganhar o reconhecimento público pelo seu importante trabalho. Ele publicou investigações geométricas sobre a teoria dos paralelos em 1840 que, nas suas 61 páginas, dão a conta mais clara de Lobachevskydo trabalho. A publicação de uma conta em francês no jornal de Crelleem 1837 trouxe seu trabalho em geometria não-euclidiana para um público amplo, mas a Comunidade matemática não estava pronta para aceitar ideias tão revolucionárias.
Lobachevskydo livreto de 1840 ele explica claramente como funciona sua geometria não-euclidiana.
Todas as linhas retas que, em um avião, sair de um ponto podem, com referência a uma determinada linha reta no mesmo plano, ser divididas em duas classes - em corte e non-corte. As linhas de delimitação do e a outra classe dessas linhas serão chamadas paralelas à linha determinada.
Aqui está o diagrama do Lobachevsky
Portanto, Lobachevsky substituiu o quinto postulado de Euclid's por:
Postulado das paralelas do Lobachevsky. Existem duas linhas paralelas para uma determinada linha através de um determinado ponto não na linha.
Lobachevsky passou a desenvolver muitas identidades trigonométricas de triângulos que realizou nesta geometria, mostrando que, como o triângulo tornou-se pequeno as identidades tendiam às identidades trigonométricas usuais.
Riemann, que escreveu sua tese de doutorado sob a supervisão de Gauss, deu uma palestra inaugural em 10 de junho de 1854, em que ele reformulou todo o conceito da geometria que ele via como um espaço com bastante estrutura extra para ser capaz de medir coisas como comprimento. Esta palestra não foi publicada até 1868, dois anos após a morte de Riemann mas era ter uma profunda influência sobre o desenvolvimento de uma riqueza de diferentes geometrias. Riemann brevemente discutidos uma geometria 'esférica', em que cada linha através de um ponto P, não em uma linha AB atende a linha AB. Nesta geometria não paralelos são possíveis.
É importante perceber que Bolyaido nem Lobachevskya descrição de sua nova geometria tinha sido provou para ser consistente. Na verdade não foi diferente da geometria euclidiana, a este respeito, apesar dos muitos séculos de trabalho com a geometria euclidiana foi suficiente para convencer os matemáticos que não há contradição alguma vez aparecem dentro dele.
A primeira pessoa a colocar a Bolyai - geometria não-euclidiana Lobachevsky no mesmo patamar que a geometria euclidiana era Eugenio Beltrami (1835-1900). Em 1868 ele escreveu um livro de ensaio sobre a interpretação da geometria não-euclidiana que produziu um modelo para a geometria não-euclidiana 2-dimensional dentro de 3-dimensional geometria euclidiana. O modelo obteve-se sobre a superfície de revolução de um tractrix sobre sua assíntota. Isso às vezes é chamado um pseudo-esfera.
Você pode ver o gráfico de um tractrix e parece que a metade superior de uma esfera de pseudo.
Na verdade Beltramido modelo estava incompleto, mas certamente deu uma decisão definitiva sobre o quinto postulado de Euclid's desde o modelo fornecido uma configuração na qual Euclid's de quatro primeiros postulados realizada, mas o quinto não segurou. Reduziu o problema da consistência dos axiomas da geometria não-euclidiana, a que da consistência dos axiomas da geometria euclidiana.
Beltramido trabalho em um modelo de Bolyai - geometria não-euclidiana do Lobachevskyfoi completado por Klein em 1871. Klein foi mais longe e deu modelos de outras geometrias não euclidianas como Geometria esférica de Riemann. Kleindo trabalho foi baseado em uma noção de distância definida por Cayley em 1859, quando ele propôs uma definição generalizada para a distância.
Klein mostrou que existem três tipos basicamente diferentes da geometria. Na Bolyai - Lobachevsky tipo de geometria, linhas retas tem dois pontos infinitamente distantes. O tipo de Riemann de Geometria esférica, linhas não têm (ou mais precisamente dois imaginários) pontos infinitamente distantes. Geometria euclidiana é um caso limite entre os dois, onde para cada linha existem dois pontos infinitamente distantes coincidentes.
Geometria não-euclidiana
ETinCiencia
O artigo é uma tradução do conteúdo deste página: History MCS ST Andrews - Non-Euclidean geometry. O conteúdo pode ser editado para estilo e tamanho.